
Nusprendžiau pasidalinti instrumentais, kuriuos naudoju nustatyti ar lažybų strategijos “veikia”. Noriu akcentuoti, kad standartiniai rodikliai, uždirbti unitai ir ROI, nebūtinai įrodo, kad strategija yra pelninga ilguoju laikotarpiu. Mes galime turėti situaciją, kai lošėjas yra pliuse, tačiau naudoja ne logiškus argumentus. Žemiau išvardintų metodų tikslas “objektyviai” atsakyti, kokia tikimybė, ar pliuse esantys statymai turi vertės. Iš karto sakau, kad neįmanoma 100% užtikrintai į tai atsakyti, tai tiesiog būdai man padedantys pašalinti žmogišką subjektyvumą.
‣ Lažybų bendrovės
‣ Kazino bendrovės
‣ Lažybų pamokos ir patarimai
‣ Lažybų brokeriai
1) p-test
Akademijoje eksperimentai dažniausiai prasideda nuo pirminių hipotezių (NULL hypothesis). Realiam gyvenime, mokslininkai neeksperimentuoja “pašaudikime su lazeriu į šitą audinį ir pažiūrėkime, kas bus”.
Pateiksiu pavyzdį iš medicinos srities. Didžioji dalis žmonių neturi piktybinio vėžio (kitaip visi sėdėtume ligoninėse), todėl vėžio tyrimuose pirminė hipotezė yra “pacientas yra sveikas”. Gydytojai analizuodami tyrimo rezultatus naudoja įvairius statistinius metodus nustatyti, ar šią hipotezę galima patvirtinti ar atmesti. Šių tyrimų metu yra galimos dviejų tipų klaidos: klaidingas hipotezės atmetimas (false negative) ir klaidingas hipotezės patvirtinimas (false positive), literatūroje dažniau rašomos kaip I ir II tipo klaidos. Taigi vėžio tyrimo atveju, I tipo klaida būtų- neteisingai atmesta hipotezė, nustatytas vėžys sveikam žmogui, II tipo- neteisingai patvirtinta hipotezė, pacientas identifikuotas kaip sveikas, nors iš tiesų turi vėžį.
Onkologijoje mums labiau rūpi išvengti II tipo klaidų, tad dažnai pirminių testų kartelės yra nuleidžiamos žemiau, ko pasekoje neretai sveikiems žmonėms neteisingai diagnozuojamas vėžys. Chemoterapijos procedūros nėra priskiriamos iš karto po pirmo pozityvaus testo, gydytojų tikslas yra kuo anksčiau identifikuoti potencialiai vėžį turinčius žmones ir tada atlikti brangesnius/tikslesnius tyrimus.
Dabar galime pažiūrėti į kitokią situaciją. Senovės graikai išmąstė, kad daug blogiau yra nekaltą žmogų pasodinti į kalėjimą (I tipo klaida), nei į laisvę paleisti nusikaltelį (II tipo klaida). Šiuo atveju mums labiau rūpi išvengti I tipo klaidų, todėl vakarietiška teisinė sistema yra pastatyta ant teiginio/hipotezės “visi žmonės yra nekalti, kol neįrodyta kitaip”. Nors visuomenė dažnai pyksta, kai į laisvę išeina “galimai” kalti žmonės, sistema yra taip sukurta, kad būtų sunku atmesti pirminę hipotezę (įrodyti kaltumą), siekiant išvengti I tipo klaidų.
Su matematika galvų nekvaršinsiu, tiesiog noriu, kad intutyviai suprastumėte, jog nuo hipotezės formuluotės parinkimo bei statistinių parametrų priklauso, kurio tipo klaidų bus daugiau/mažiau. Klaidingų hipotezės atmetimų/patvirtinimų išvengti neįmanoma!
Taigi dabar klausimas, kokią hipotezę reikėtų iškelti lažyboms? Formuluojant pirminės hipotezes, rekomenduojama sakyti, kad viskas pasaulyje vyksta normaliai, tad būkime naivūs ir teikime:
“lažybų bendrovių siūlomi didžiausi koeficientai atitinka tikrąsias įvykių tikimybes”
Norėčiau atkreipti dėmesį, kad ši hipotezė yra specialiai padaryta per naivi! Žemiau pateikiu atsitiktinių NBA varžybų paskutinius koeficientus. Pagal hipotezės formuluotę, nesvarbu ar lošėjęs statys už Lakers pergalę @1.42 dafabet ar už Rockets @3.27 coolbet, ilgalaikėje perspektyvoje jo grąža bus arti nulio. Realybėje daug didžiausius siūlomus koeficientus siūlančių bendrovių nėra patikimos, normalios bendrovės seka vienas kito koeficientus, tad “realistiškiau” būtų teigti, kad ilgalaikėje perspektyvoje lošėjo grąža bus šiek tiek neigiama, apytiksliai lygi maržai paskaičiuotai iš didžiausių koeficientų.
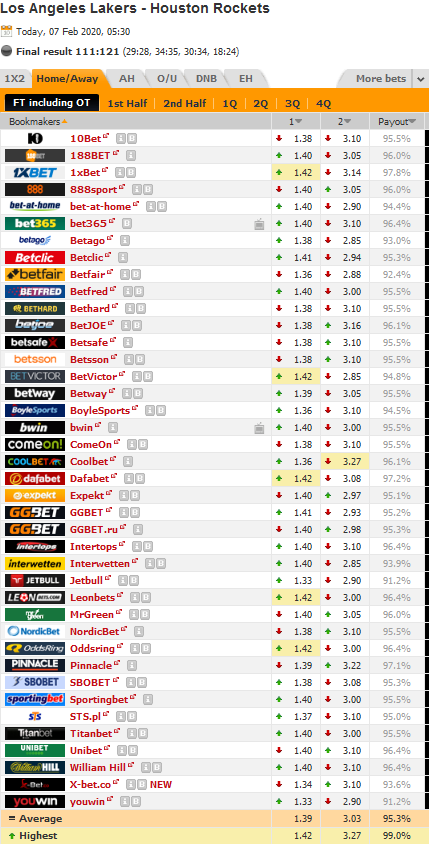
Priminsiu, šiuo atžvilgiu I tipo klaida būtų klaidingas hipotezės patvirtinimas- nors strategija ir yra pelninga, mes nusprendėme, kad joje vertės nėra- tiesiog neuždirbame pinigų. II- tipo klaida, atmetame hipotezę- pradedame statyti pinigus ir keliaujame į minusą. Pralošti pinigų (II tipo klaida) yra daug skaudžiau nei neuždirbti pinigų (I tipo klaida), todėl mes pirminią hipotezę suformulavome naivesnę nei ji yra realybėje.
Eksperimentas- atliekame statymus ant vertės turinčių įvykių. Tuomet apskaičiuojame p vertę (p value arba p test), kuri mums pasako, kokia tikimybė, kad hipotezė teisinga. Jei p yra labai mažas, tuomet hipotezė yra atmetama, o jei p didelis- hipotezė yra patvirtina.
Internete pilna informacijos, kaip apskaičiuoti p-test (yra ir kitų metodų). Aš susidomėjusiems rekomenduočiau skirti laiko pasimokyti statistikos. Visgi likusiems duosiu paprastesnį variantą- Joseph Buchdahl yra padaręs reikiamas skaičiuokles excel’iui, tad kas norite pasitikrinti savo strategijas, dokumentą galite atsisiųsti (http://www.football-data.co.uk/blog/model_testing.php), dešinėje pusėje pamatysite “Test your bets”, paspaudus leis atsisiųsti excel failą.
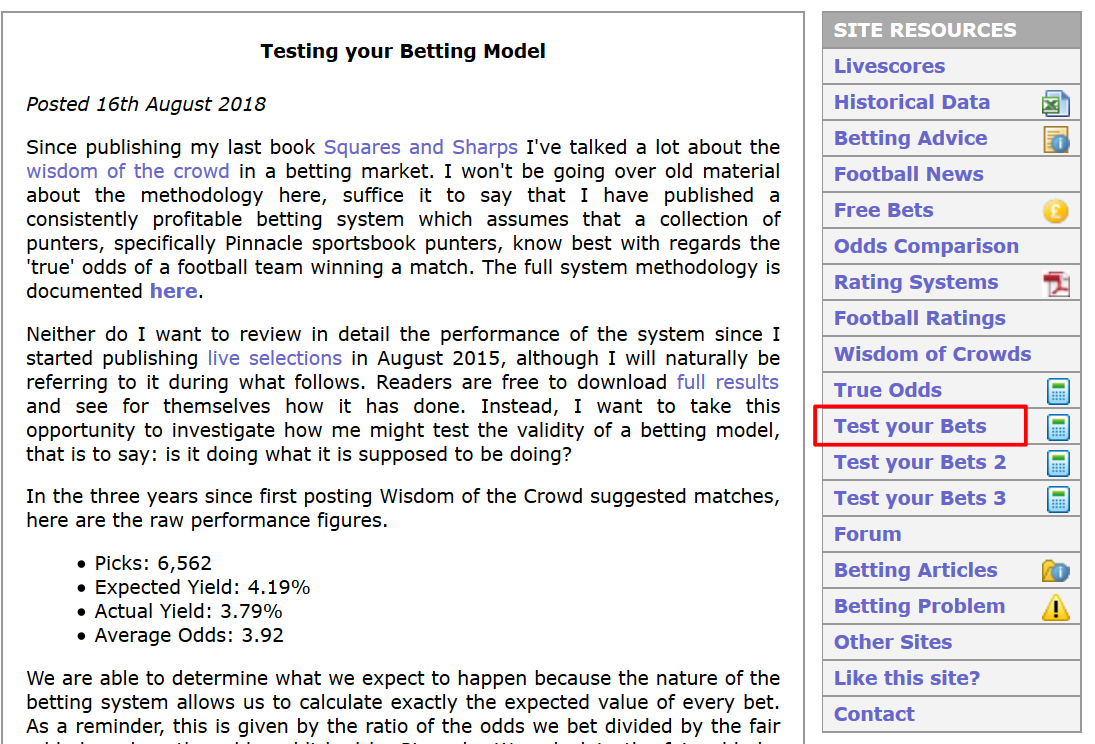
Tad patikrinkime kaip naudotis šiuo dokumentu ant tikrų duomenų. Aš gavau Kaunas sutikimą, kad galėčiau šios testus atlikti ant jo viešų statymų (https://www.statymai.com/tipster/kaunas). Čia nėra jo kaip prognozuotojo reklama!
P testo tikslas, patikrinti, kokia tikimybė, kad turite pelningą strategiją, tad pirma statymus reikia normuoti į vieną unitą. Taip, vieni statymai yra vertingesni už kitus, tad ant jų didesnį % nuo banko galima dėti, o ant vertės turinčio 20 koeficiento gali ir nekilti ranka pastatyti tokią pačią sumą, kaip ant 1.9 kofo. Visgi šių testų tikslas patikrinti ar tu turi pranašumą prieš lažybų bendroves, o ne optimizuoti ROI.
Kaunas atveju, dauguma jo statymų daryti po 10 unitų, tad iš esmės jis statė lygiais unitais (flat unit stacking). Paklaida nėra didelė, statant po 1 unitą ROI yra 2.3% (29.58 unitai), o ne 2.32% (284.19 unitai). Visgi vardan tikslumo, žemiau visur naudosiu skaičiavimus pagal jos rezultatus sunormuotus į vieną unitą.
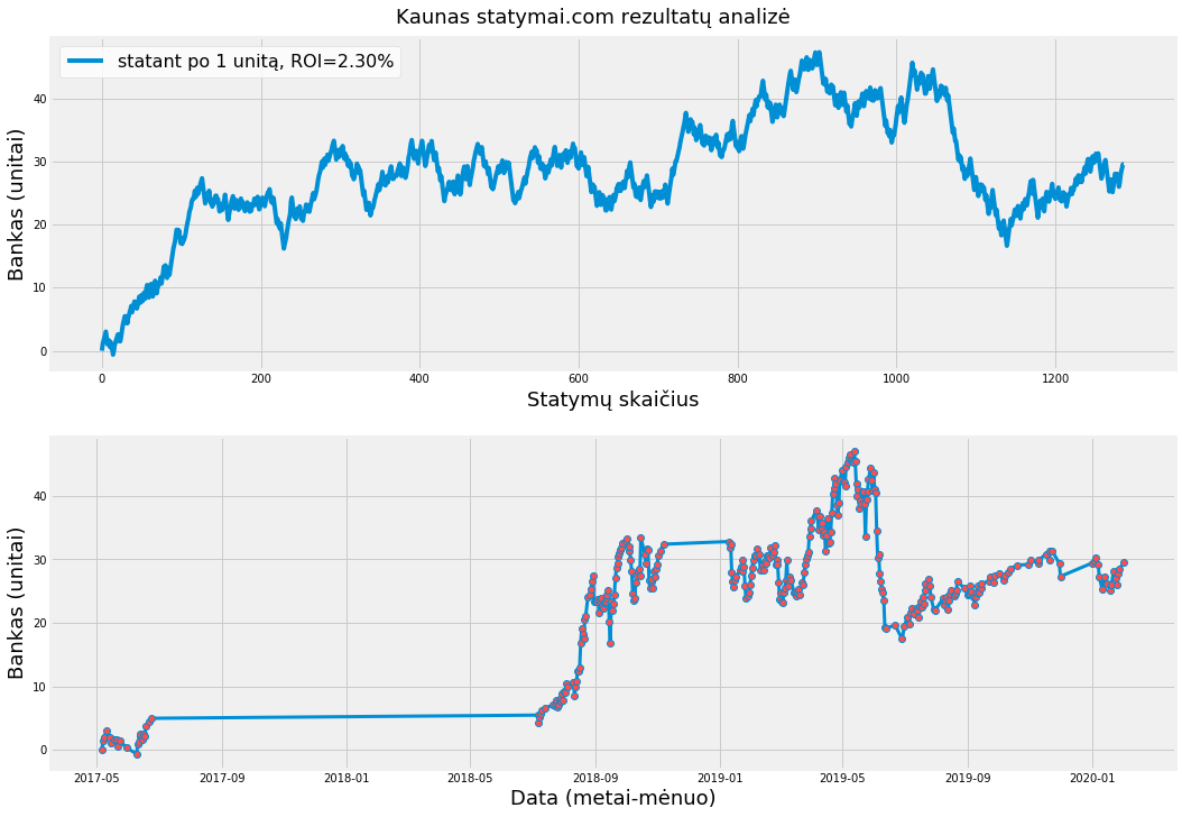
Kaunas rezultatų laikinė analizė suteikia puikią progą pažvelgti, kaip ilgalaikėje perspektyvoje atrodo lažybų variacijos. Tad dabar galite atidaryti atsisiųstą excel dokumentą ir įveskite visus Kaunas rezultatus.
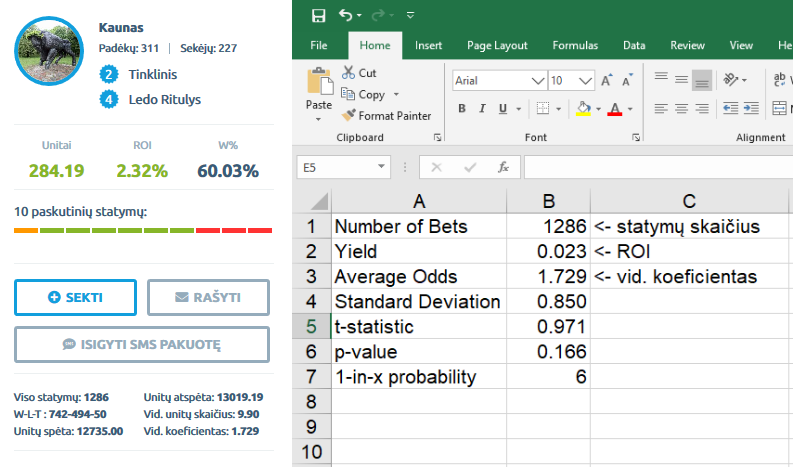
Kaip matote mums rašo, kad yra 16.6% tikimybė, kad Kaunas rezultatus lėmė atsitiktinumas. Moksliniuose straipsniuose yra įprasta naudoti bent p=0.05 kriterijų, kai p vertė mažiau už 0.05 (tikimybė <5%), hipotez="" yra="" atmetama="" primenu="" m="" s="" atveju="" mes="" norime="" atmesti="" kad="" la="" yb="" bendrovi="" koeficientai="" parodo="" tikr="" sias="" tikimybes="" tad="" i="" vada="" tokia-="" 16="" 6="" tikimyb="" span="">Kaunas kaip prognozuotojas, sporto įvykių tikimybes žino geriau nei sporto lažybų bendrovės. Iš patirties sakau, kad p=0.05 pramušti yra labai sunku, tad 16.6% kaip lažyboms yra tikrai neblogas rezultatas. Ir šiaip, po 1000 statymų nebūti minuse jau yra vertas aplodismentų pasiekimas!
Visgi šio testo papildoma funkcija yra palyginti skirtingas statymų strategijas, kurios turi skirtingą kiekį statymų bei ROI. Tad detaliau paanalizuokime Kaunas statymų pelningumą pagal koeficientų dydžius.
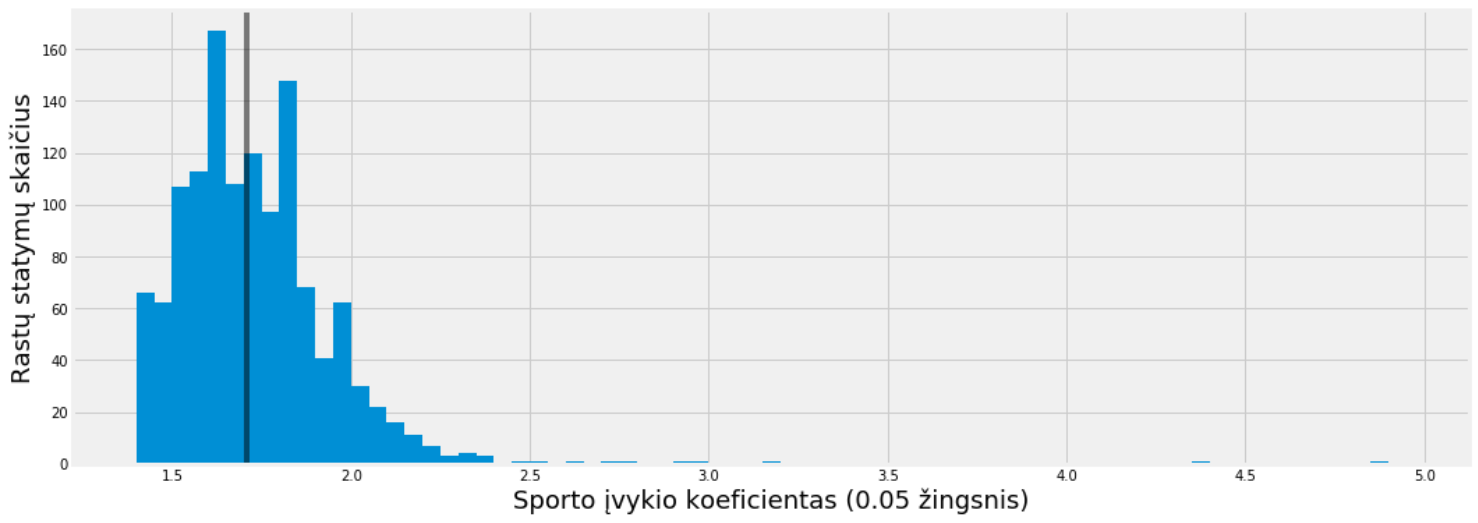
Kaip matote Kaunas yra nedidelių koeficientų mėgėjas. Daug lošėjų teigia, kad maži koeficientai ilgalaikėje perspektyvoje neatneša pelno (kiekvienas turi savo nuomonę, nuo kada jis skaitosi mažas). Tad panaudokime p-test išsiaiškinti, gal Kaunas žino kažką, ko nežino kiti.
Koeficientų mediana @1.71 leidžia Kaunas statymus padalinti į dvi beveik lygias dalis.
* (koeficientas <1.71) 650="" statymai="" 18="" 11="" unitai="" roi="2.79%," vid="" kofas="" 1="" 56="" p-vert="" 0="" 169="" span="">
* (koeficientas >=1.71) 636 statymai, 11.47 unitas, ROI= 1.80%, vid. kofas: 1.90, p-vertė 0.316
Mano nuostabai atrodo, kad statymai su mažesniais koeficientais atrodo patikimesni (mažesnė p vertė). Čia reiktų paminėti, kad aš analizuoju Kaunas statymus be jo komentarų. Iš aukščiau pateiktų paveikslėlių matosi, kad jis du kartus buvo atlikęs ilgesnes pertraukas tarp statymų įkėlimų. Tad nėra korektiška nagrinėti beveik 3 metų statistiką bendrai, Kaunas kaip lošėjas, tikriausiai keitėsi. Visgi savo įdomumui patikrinau aukštesnių koeficientų grąžą.
* (koeficientas >=1.85) 375 statymai, 31.58 unitai, ROI= 8.42%. vid kofas: 1.99, p-vertė 0.051
Na štai, kai Kaunas statymai su aukštesniais koeficientais jau beveik moksliškai paneigia pirminę hipotezę!
Čia Kaunas komentaras:
"Žinoma, gali naudoti mano statymų statistiką savo post'ui.
Tik norėčiau akcentuoti: aš nesu joks prognozuotojas, tipsteris ar pan. Prognozių rašymas buvo (o gal ir tebėra) man tam tikras eksperimentas, iššūkis. Kodėl?
Visų pirma, man nėra įprastos prognozių rašymo taisyklės. Realybėje dažnai atlieku statymus, kurie minėtoms taisyklėms prieštarauja.
Antra, mano prognozių rašymui turėjo įtakos grįžtamoji vartotojų reakcija. Jeigu jos nebūtų buvę, gal ir prognozes būčiau rašęs kitas, ir rezultatus turėčiau kitokius.
Taip pat turėjo įtakos ir skelbti mėnesio geriausių prognozuotojų konkursai: kai atsiranda šansas pakovoti dėl prizinės vietos, nevalingai keiti ir sau įprastą prognozių rašymo stilių (renkiesi daugiau ar mažiau įvykių, taip pat - rizikingesnius ar mažiau rizikingus įvykius).
Reziume: kaip "ėjusiam pro šalį" ir nusprendusiam sudalyvauti prognozių rašyme, mano rezultatai, sakyčiau, tikrai neblogi. Galbūt jie būtų ir geresni, jeigu galėčiau sistemingai skirti jiems laiko. Dabar dažniausiai mane veda įkvėpimas.
Antra vertus, negali žinoti, kaip man sektųsi, jeigu laiko prognozėms turėčiau pakankamai. 2019 m. birželį mano statistikoje yra riebus 233,39 unitų minusas. Beveik visi statymai - iš tinklinio, kuris iki tol buvo atnešęs daugiausiai pliuso. Negalėjau suprasti, kas tą mėnesį vyko: vienas po kito degė daugybė logiškų prognozių. Todėl tinklinio teko visai atsisakyti. Matyt, sėkmės/nesėkmės faktorius tąkart suveikė prieš mane - kito paaiškinimo neturiu.
”Mano komentaras:
“Tinklinyje Kaunas yra bendrai pliuse. Tad 2019 metų birželį tikriausiai buvo regresija link vidurkio (regression to mean). Čia kaip Žalgirio žemas 3-taškių pataikymas EL sezono pradžioje, anksčiau ar vėliau tie pataikymo % artėja prie normalių vidurkių. Čia atskiros temos verta diskusija, ką daryti su ilgalaikiais pliusiniais ir minusiniais laikotarpiais.
”Reziumuojant, p-test nėra visų problemų sprendimas- jis leidžia kažkaip objektyviai palyginti rezultatus tarp strategijų su skirtingais statymų kiekiais, uždirbtais unitais ir ROI. Norėčiau akcentuoti, kad mes skaičiuojame, kokia tikimybė, kad lažybų strategija yra pelninga (one-tailed test). Šis metodas neleidžia apskaičiuoti atsitiktinumo tikimybės, kai turime minusinį ROI (Kaunas 2018 birželis). Patys suprantate ir laiminčios strategijos turi nesėkmingus ruožus. Lažybose manau sveika būti skeptikų, tad radus pelningą strategiją ar prognozuotoją, šis testas padeda gauti šiek tiek perspektyvos, kiek tuos rezultatus galėjo lemti sėkmė, kuri lažybose ir gyvenime buvo ir bus!
2) brier-score
1964 Šermanas Kentas (Sherman Kent) dirbdamas su žvalgybos institucijomis nusprendė poetus atskirti nuo matematikų. Žvalgybininkai pristatydami įvykių ataskaitas dažnai naudovo žodžius “labai tikėtina”, “galimai”, “maži šansai” ir pan. Problema, kad labai sunku objektyviai palyginti skirtingų ekspertų įžvalgas- vienam “labai tikėtina” gali reikšti 90%, kitam 75%. Tad jis pasiūlė šiuos žodžius susistemizuoti (Words of estimative probability).
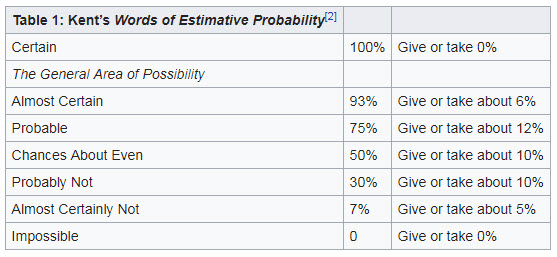
Lažybų prognozėse įprasta sutikti argumentus “šitie labiau nori” ar “aniems labiau reikia”. Mano asmeninis požiūris- visuomet prieš atliekant statymą reikia užrašyti, kokią tikimybę tam įvykiui skiri. Jei vieni labiau nori, tai kiek tokia įžvalga verta %? Pavyzdžiui, statant su 1.83 koeficientu prognozuoju 58.5% laimėjimo tikimybę, toks statymas mano akimis turės 7% vertę. Tai ne tik leidžia sekti prognozuotą grąžą, bet ir su laiku patikrinti, ar tavo prognozės yra per daug optimistiškos ar kaip tik pesimistiškos.
Tam tikslui yra labai patogu naudoti (brier score), toliau žymėsiu BS. Tai yra matematinis būdas nusakyti, ar prognozuotojas yra tikslesnis už atsitiktinumą. Skaičiavimo procedūrą galima atlikti excel ar google sheet:
1) užsirašome įvykio proporcinę tikimybę, pvz. 58% -> 0.58 (col B), tai bus mūsų tikrinamas modelis,
2) tikimybė pagal koeficientą (col A), pvz. 1.83 -> 1/1.83= 0.55 (col C), tai bus palyginamasis modelis (ta pati hipotezė, kaip p-test, teigiama, kad koeficientai parodo tikrąsias tikimybes),
3) užrašome įvykio baigtį: 1-sėkminga, 0- nesėkminga (col D),
4) paskaičiuojame kvadratines klaidas testuojamam ir palyginamajam modeliams (col E ir col F). Tarkime buvo prognozuota, kad statymas turi 58% laimėjimo tikimybę. Pergalės atveju (1 - 0.58)^2 = 0.18 baudos taškai bus gauti gauti, o pralaimėjimo (0 - 0.58)^2 = 0.34 taškai.
5) paskaičiuojame baudos taškų vidurkius prognozėms ir lažybų bendrovėms, tai bus BS-1 spėjimų ir BS-REF lažybų bendrovių (col E ir col F vidurkius).
Pateikiu keletą skaičiavimų pavyzdžių.
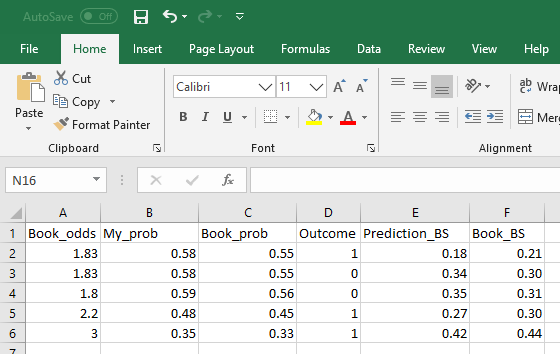
Jei BS-1 yra didesnis už BS-REF, tuomet tai yra labai konkretus indikatorius, kad prognozuojamos tikimybės yra mažiau tikslios nei spėjimas aklai.
BS tau duos labai daug baudos taškų, jei pavyzdžiui ant taškų totalo dėsi 70% tikimybę. Sėkmės atveju gausi 0.09 baudos taškus, o nesėkmės 0.49. Aklai spėdamas, kad toks statymas turi 50% tikimybę praeiti, gausi po 0.25 baudos taškus tiek laimėjimo tiek pralaimėjimo atveju, tad apskaičiavus vidurkius BS-REF bus mažesnis už spėjimų BS-1.
Daniel Kahneman knygoje “Thinking fast and slow” pastebėjo, kad mes daug skaudžiau vertiname praradimus nei laimėjimus. Labai lengva pradėti dvejoti modeliu ar prognozuotoju, kai jis turi minusinį laikotarpį, tačiau labai retai kam iškyla abejonių, kai yra išgyvenamas labai pelningas laikotarpis. BS metodo tikslas apsaugoti lošėję nuo per daug optimistiškų prognozių, net kai jis yra pliuse (bent aš tokiais tikslais jį naudoju).
Pabaigai noriu akcentuoti, kad nei vienas nei kitas metodas, negarantuoja, kad pavyks rasti pelningų strategijų. Galbūt sutapimas, bet šiam puslapyje neseniai buvo pasidalinta Billo Benterio istorija (galvojau, gal kada reiktų ir apie jį parašyti). Gaila, kad video pasakojo tik apie tai, kiek jis pinigų išlošė ir, kad kompiuterius naudojo. Billas yra net viešai parašęs straipsnį apie savo lažybų modelį žirgų lenktynėms (galite išgooglinti “Computer Based Horse Race Handicapping and Wagering Systems: A Report”). Jis 1994 publikuotas, tad tikrai nebeveikia!
Ne vien kompiuteriuose buvo jo sėkmės paslaptis. Jis pastebėjo, kad jei naudoji daugiau skirtingų parametrų ir modelių, tuomet gali gauti daug tikslesnes prognozes (ką iš esmės dabar daro visi). Kai kurie lošėjai, neoficialiai šią įžvalgą vadina Benter method. Priimdamas sprendimą, ar pradėti statyti tikrus pinigus ant naujos strategijos, aš visuomet ją patikrinu, ką man meta p-test, brier score ir kiti metodai. Tobulų strategijų nėra, tačiau jei strategija praeina daugumą tavo jai taikytų testų, tuomet tikrai daug drąsiau jautiesi prieš atlikdamas statymus.
Autorius: Tomas (Tigfiend)















.jpg?v=1.014689135)














